鋯合金具有較低的熱中子吸收截面、優異的耐腐蝕性和良好的力學性能與加工性能,被廣泛應用作核反應堆的包殼材料和結構材料[1-3]。鋯合金在室溫下為hcp結構的α-Zr,其結構對稱性較低,獨立滑移系較少,塑性變形過程中通常需要滑移和孿生協同開啟[4,5]。其中,柱面滑移的臨界剪切應力(CRSS)相對其他滑移系最小,是鋯合金變形過程中最容易開啟的滑移系[6],錐面滑移和基面滑移開啟以協調變形[7,8]。當晶體取向不利于滑移時,孿晶開啟并使晶粒產生固定角度的取向改變[8,9]。鋯合金帶材在加工過程中易形成織構,導致材料各向異性,進而引起室溫沖制過程發生開裂。因此,研究鋯合金在沖制過程中的織構演變,分析沖制過程中的應變路徑和變形機制之間的關系,對揭示沖制過程中影響開裂的關鍵機制、明確開裂敏感的晶粒取向具有重要的理論意義和應用價值。定位格架由鋯合金帶材沖制而成,沖制過程中的應變路徑與成形零件的幾何形貌、成形過程中的工藝條件以及材料性質等多種因素有關。Lei等[10]設計了近似U形的鋯合金剛凸結構件,發現沖制后在剛凸的邊緣發生開裂,破裂位置的應變路徑為近平面應變路徑。鄧振鵬等[11]模擬了鋯合金帶材沖制過程,發現增大凸凹模間隙、減小摩擦系數,可有效降低帶材沖制后的極限應變,利于成形。鋯合金的各向異性使其在塑性變形過程中應變路徑發生偏轉,隨著材料屈服表面指數的下降,成形過程中的應變路徑從線性變為非線性,并向平面應變路徑發生偏轉[12]。此外還有學者[13-14]采用多工步沖制工藝,改變應變路徑消除定位格架沖制開裂的問題。然而這些研究主要討論沖制過程中的宏觀應變路徑,對應變路徑與織構演變及微觀變形機制的內在關系尚不明確。目前,針對鋯合金微觀變形機制及織構演化的研究多集中于簡單加載條件(如單向拉伸和軋制)。其中,Deng等[15]通過單向拉伸實驗結合粘塑性自洽(visco-plasticself-consistent,VPSC)模型解釋了Zr-4合金的各向異性屈服行為主要源于不同方向加載時柱面滑移的開啟量不同。Liu等[16]發現基面滑移和孿生開啟量的差異導致了Zr-4合金板材單向拉伸時的各向異性硬化。Luan等[17,18]研究了Zr-1.0Sn-0.3Nb板材壓縮和軋制過程中的微觀組織及織構演變。Knezevic等[19]發現大應變變形時,Zr的典型軋制織構的形成依賴于基面滑移的開啟。Cao等[20]研究了Zr-Nb-Mo合金在冷軋過程中的變形機制,結果表明錐面滑移是軋制到大變形量條件下協調厚度方向變形的主要滑移機制。沖制過程在不同位置的應變路徑較復雜,針對這一復雜加載條件下的微觀機理研究目前尚不多見。
本工作采用自研沖制模具開展Zr-4合金帶材的沖制實驗,采用電子背散射衍射(EBSD)方法測試了沖制深度為1.16mm的沖制元件在凹模圓角、斜壁和凸模圓角3個位置的織構變化,并利用晶內取向差轉軸法(IGMA)明確了不同位置開啟的變形機制差異。通過宏觀有限元(FEM)-粘塑性自洽(VPSC)間接耦合模型,分析應變路徑對沖制過程中的織構演變及變形機理的影響,揭示影響沖制開裂的關鍵機制,這對深入理解鋯合金帶材沖制過程的織構形成機理、降低沖制開裂趨勢具有重要的理論意義和工程應用價值。
1、實驗方法
1.1實驗材料
本實驗采用某公司生產的0.457mm厚退火態Zr-4合金帶材,主要化學成分為Zr-1.2Sn-0.2Fe-0.1Cr(質量分數,%)。將帶材切割成小樣品,尺寸為30mm?20mm?0.457mm(RD-TD-ND,其中RD代表帶材的軋制方向,TD代表帶材的寬度方向,ND代表帶材的法向方向)。退火態Zr-4合金初始帶材為無孿晶的再結晶等軸晶組織,晶粒尺寸約為5.0μm(圖1a)。初始織構為基面的雙峰織構,c軸與ND方向成約20?傾斜,織構強度為4.0mud。一般用Kearns系數[21](Kearnsfactor)表征材料內部晶粒的取向分布狀態,定義為極軸沿特定方向排列的晶粒的有效百分數,它代表了試樣內部晶粒基軸沿不同方向分布的幾率,由下式計算:

式中,F為Kearns系數,φ為晶粒的c軸與特定方向的夾角,Iφ為傾斜角度φ時的平均強度。初始帶材的Kearns系數為Fr=0.084,Ft=0.188,Fn=0.728。其中,Fr、Ft和Fn分別表示帶材沿軋向、寬向和法向的Kearns系數。

1.2Zr-4合金沖制實驗
圖2所示為沖制實驗模具示意圖及模具關鍵參數。將沖制模具(圖2a)安裝在沖壓機床上,樣品放置在凹模上進行沖制。沖制模具尺寸如圖2b所示,沖頭尺寸為長10.3mm,寬3.8mm,凹模為長12.1mm,寬5.4mm,深度1.62mm,沖頭圓角半徑Rp=0.15mm,凹模圓角半徑Rd=0.6mm。進行沖制深度為1.16mm的沖制實驗,分析沖制后樣件在不同位置的織構變化。

1.3沖制樣件典型位置EBSD及成形深度測試
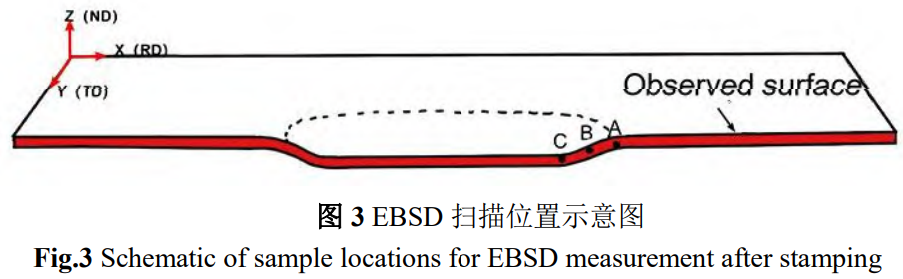
沖制后樣件沿著軋制方向切開,在縱截面選取3個區域(A、B、C)進行EBSD觀測,如圖3所示。A、B、C分別位于凹模圓角區、斜壁區及凸模圓角區,x、y、z方向分別為帶材的軋制方向、寬度方向和法線方向,圖中紅色區域為實驗的觀測面(RD-ND面)。EBSD樣品采用機械拋光+電解拋光方法制備,電解拋光液中乙醇和高氯酸的體積比為9:1,電解溫度-40℃,工作電壓30V,電解時間3min。利用Mira3XMU場發射掃描電鏡(SEM)對變形前后的樣品進行EBSD觀測,步長0.2μm,使用Aztec軟件進行數據采集,實驗數據通過HKLChannel5軟件進行分析處理。
為有限元模擬提供準確的邊界條件,選用白光干涉實驗測量沖制樣件的深度。白光干涉儀是以白光干涉技術為原理,對器件表面進行非接觸式掃描并建立表面3D圖像,從而實現器件表面形貌測量的光學檢測儀器[22]。本實驗采用MicroXAM3D白光干涉儀,通過MicroXAM操作軟件和Qport數據分析軟件進行結果處理。
1.4Zr-4合金沖制有限元模型建立
根據實際工件尺寸建立有限元模型,模型包括凸模、壓邊圈、帶材和凹模,如圖4所示。帶材單元采用Belytschko-Tsay殼單元網格,網格尺寸為0.18mm,共計96941個單元。模具定義為剛體,沖壓過程分為壓邊階段與成形階段。壓邊階段設置壓邊圈的速率為150mm/s,下行直至將板料壓到凹模上為止;成形階段為了與實際生產的成形過程保持一致,設置凸模的速率為150mm/s,為了保證壓邊圈對板料的壓邊作用,設置壓邊圈的壓力為3kN。模型中接觸類型設置為contact_forming_one_way_surface_to_surface,帶材與模具之間的摩擦系數均設置為μ=0.125。

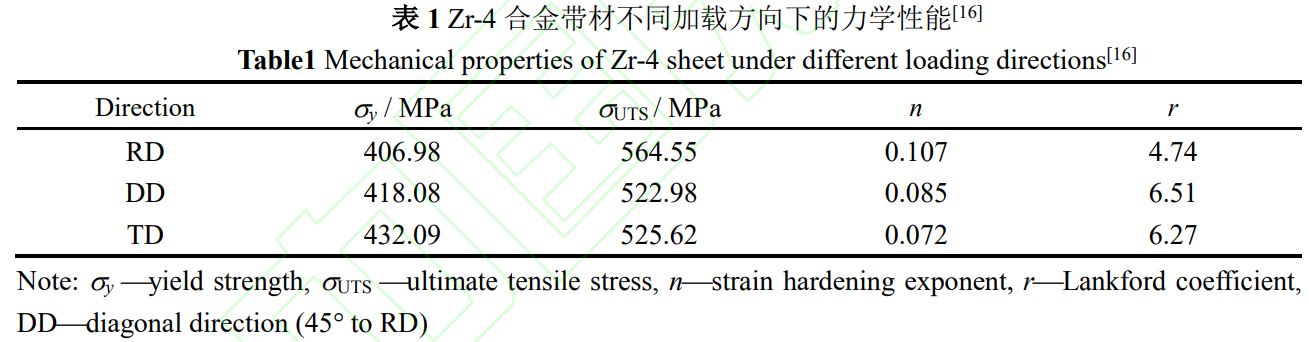
Zr-4合金帶材的屈服模型選用Barlat89屈服準則(36*MAT_3-PARAMETER_BARLAT)。之前的研究工作[16]已經測試了Zr-4合金帶材的各向異性,因而采用Zr-4合金帶材的不同加載方向的力學曲線作為此模型的輸入。屈服強度、抗拉強度、n值和r值如表1[16]所示。其中,n為應變硬化指數(strainhardeningexponent),r為各向異性系數(Lankfordcoefficient)。當加載方向從RD轉變到TD時,屈服強度從406.98MPa增加到432.09MPa,抗拉強度從564.55MPa降低到525.62MPa。沿RD方向的n值最大為0.107,r值最小為4.74。TD方向的硬化能力最差,n值最小為0.072。沖制過程的有限元模擬通過控制凸模移動的位移來完成。
1.5Zr-4合金晶體塑性模型建立α-Zr中最優先開啟的滑移系為柱面滑移。Akhtar等[23,24]認為,柱面滑移的臨界剪切應力相對其他滑移系最小,這是柱面滑移系主導變形的最重要的原因。此外,基面滑移、錐面滑移及{101?2}<1?011>拉伸孿生是協調變形而開啟的變形機制。因此在VPSC模型中選用上述4種變形機制,通過擬合不同單向加載方向的真實應力-應變曲線,對比拉伸后的實驗織構與預測織構,確定適合Zr-4合金單向拉伸條件下的VPSC模型硬化參數,結果如表2所示[16]。該組模型參數可很好地表征各向異性的力學行為,預測的變形機制開啟準確,因而本工作中也選用此組模型參數來預測沖制過程的織構演變和變形機制。

2、實驗與模擬結果
2.1沖制實驗結果
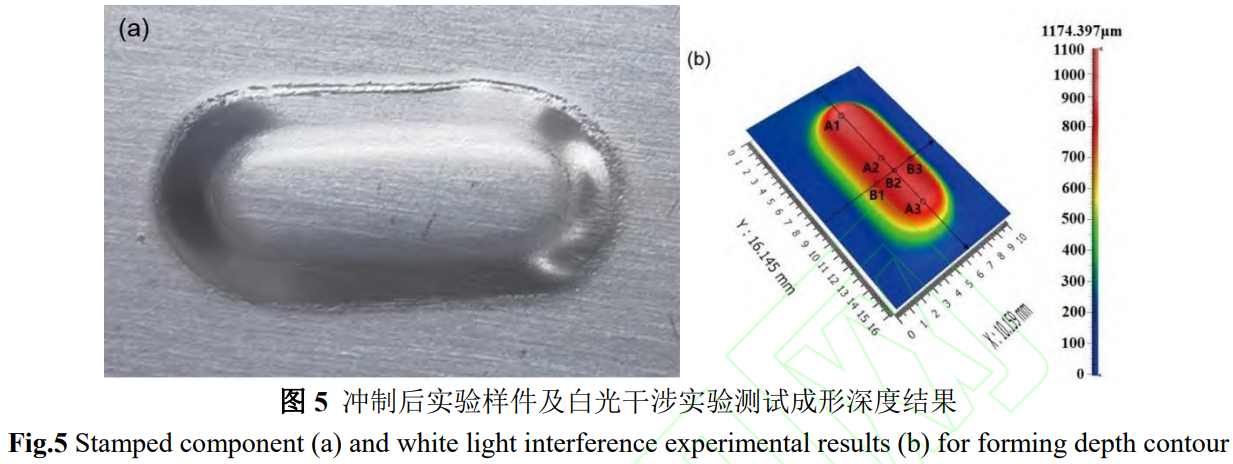
對Zr-4合金帶材進行沖制實驗,控制沖頭位移1.16mm,圖5a所示為沖制樣件。沖制后在凸模圓角位置發生開裂,表面產生了明顯的裂紋。為了準確測量沖制樣件的深度,為有限元模擬提供準確的邊界條件,進行了白光干涉實驗,實驗結果如圖5b所示,沿縱截面3個位置A1~A3的深度分別為1.167、1.127和1.147mm,沿橫截面3個位置B1~B3的深度分別為1.177、1.157和1.177mm,取6個位置的平均值,經計算所對應的成形深度為1.159mm。
2.2Zr-4合金沖制后組織和織構的變化
圖6為沖壓后3個位置(A:凹模圓角;B:斜壁;C:凸模圓角)的EBSD結果。圖6a為凹模圓角處的晶粒取向圖,晶粒沿著沖制后的伸長方向被拉長,晶粒取向以<0001>//ND方向為主(紅色晶粒),晶內出現少量其他顏色(藍色和綠色)透鏡狀的新取向。經過圖6d孿晶界標定結果可知,孿晶為{101?2}(1?011)拉伸孿晶(ETW),結合ImageJ軟件測量得ETW相對面積分數為1.896%。相應地,由于ETW的產生,板材的初始織構發生偏轉,形成了在RD方向上的強度集中,如圖6g所示。Fr由于孿晶的生成從初始的0.084增加到了0.088。
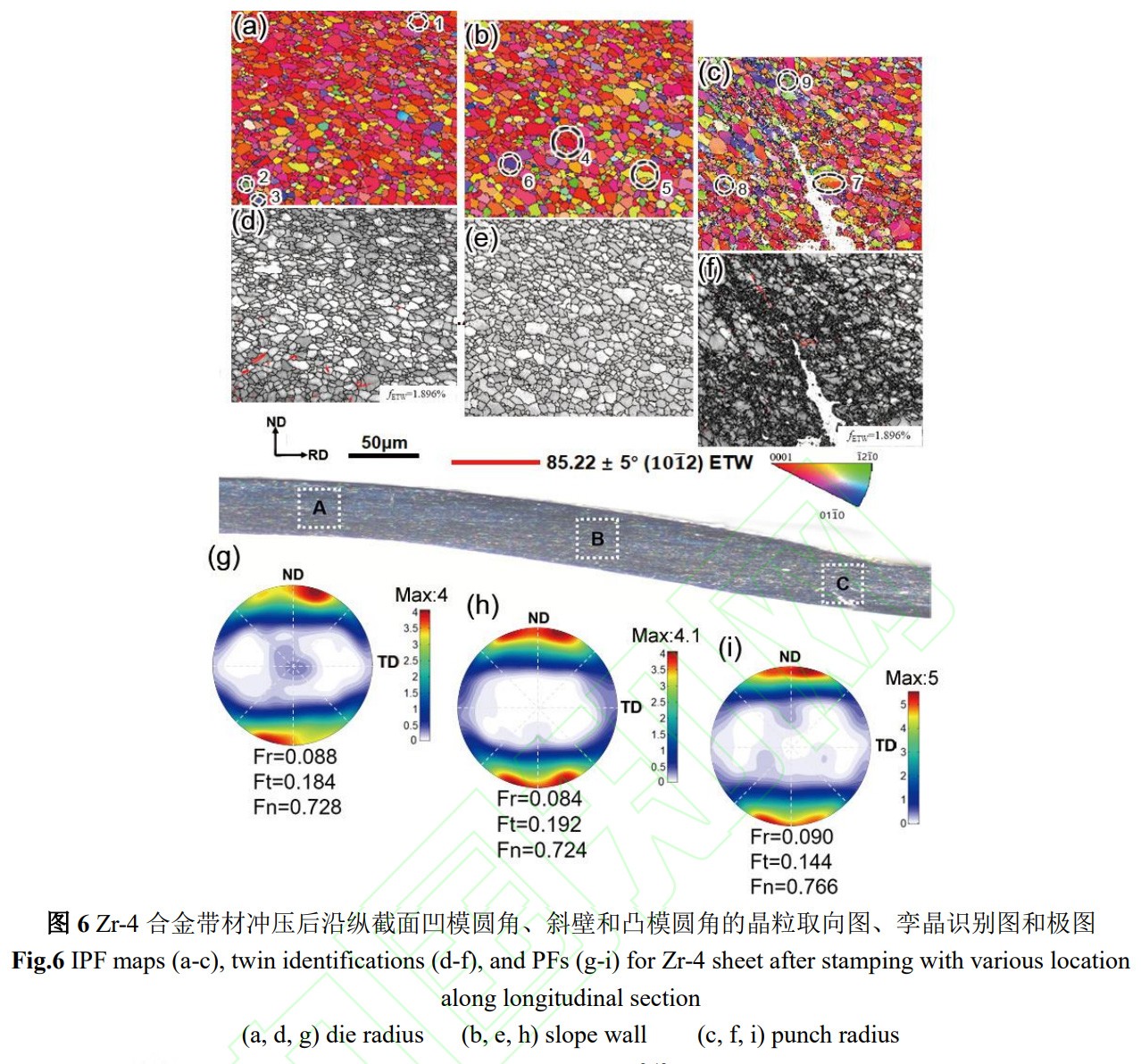
斜壁段的晶粒取向圖如圖6b所示,晶粒被拉長,晶粒取向以<0001>//ND方向為主(紅色晶粒),但相對于初始織構,藍色和綠色取向的晶粒分數稍微增加。從圖6e中看出,斜壁段沒有孿晶生成。織構類型仍保持雙峰織構,Ft由0.188增加到了0.191,Fn由0.730降低到0.726。晶粒c軸從ND向TD略微傾轉,但幾乎與初始織構一致。
圖6c是凸模圓角破裂位置的晶粒取向圖,可以看出晶粒在沖制破裂位置處發生明顯的碎化,內部出現了較多的小角度晶界。晶粒取向仍以<0001>//ND方向為主(紅色晶粒),并能觀察到有少量孿晶生成,經標定,仍為{101?2}(1?011)拉伸孿晶,孿晶分數小于凹模圓角處,約為0.689%(圖6f)。圖6i所示基面織構顯著增強,發生了更為明顯的向法向的集中,Fn明顯增加,從0.730增加到0.766;Ft發生明顯降低,從0.188降低到0.151。表明變形晶粒的c軸從TD向ND發生偏轉。
2.3有限元模擬結果
圖7所示為沖制后的Zr-4樣件沿縱截面的實際測量厚度與模擬厚度的對比。圖7a所示為有限元預測的壁厚分布云圖,壁厚最小的位置與實際破裂位置一致,均位于凸模圓角底部。隨著位置由凹模圓角變化到斜壁,壁厚呈先降低再升高的趨勢,減薄主要發生在近凹模圓角位置。隨著斜壁處到凸模圓角處,壁厚一直減小。為了更直觀的對比縱截面方向的厚度分布情況,沿縱截面選取了10個點測量厚度,10個點的具體位置與板材厚度變化的數值模擬對比如圖7b所示。結果表明,在凸模圓角處厚度減薄最明顯,減薄最大的位置實測厚度為0.406mm,預測厚度為0.410mm。凹模圓角的厚度為0.445mm,數值模擬厚度0.449mm,數值模擬結果與實驗測量結果吻合得較好,也驗證了采用的本構模型的準確性。Zr-4合金帶材在沖制變形后,凸模圓角處應變大,造成了應力集中,使得減薄嚴重,造成了沖制破裂。

圖8所示為選取不同位置處有限單元的正應變分量演化及應變狀態。圖8a中,隨著材料流入模腔內,凸模圓角的變形應變沿著帶材軋制方向與沿厚度方向的應變大小相等,方向相反,寬度方向應變分量εyy近似為0,正應變εxx=0.15和εzz=-0.15,其中,εxx、εyy、εzz分別為沿著RD、TD、ND方向的正應變。凹模圓角位置處的受力狀態如圖8b所示,εxx?0,εyy<0、εzz<0,最后時刻沿RD的正應變約0.09(圖8a),說明凹模圓角位置沿軋制方向伸長,寬度方向和厚度方向收縮。斜壁段的應變狀態與凹模圓角相似,軋制方向應變分量為正,寬度方向和厚度方向為負,且由于變形量非常小,應變分量值也較小。

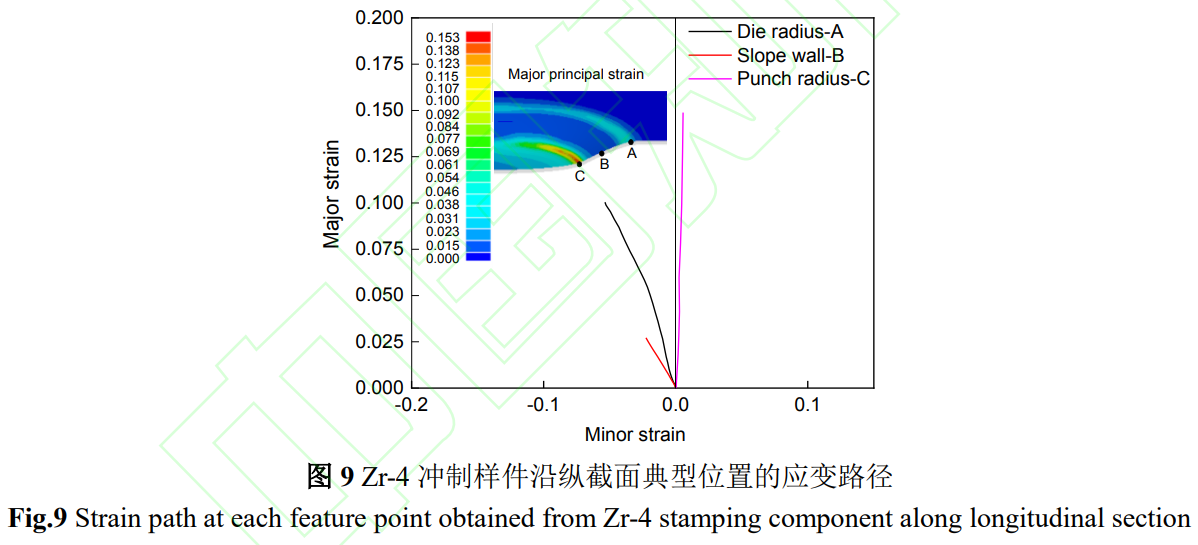
在成形過程中,典型位置A、B和C的應變路徑及3個位置的主應變分布云圖如圖9所示。實際樣件開裂位置(凸模圓角C)的應變路徑為近平面應變,最大主應變高于A和B位置,說明變形后減薄最嚴重的區域發生的應變路徑為平面應變。斜壁段B位置的應變路徑為單向拉伸,主應變?1為正,次應變?2為負。凹模圓角A位置的應變路徑為單向拉伸路徑,最大主應變約為0.1,相較于斜壁,應變更大,路徑更偏向于平面應變。綜上,沖制樣件的凸模圓角位置的受力狀態為平面應變狀態,路徑為平面應變路徑,應變值最大,極易超過成形極限曲線的平面應變特征點(FLD0),進而發生樣件的沖制開裂。
3、分析討論
3.1應變路徑對沖制過程變形機制的影響(IGMA分析)
IGMA是確定材料變形過程中滑移系開啟的一種方法[25],基于IGMA分析可以獲得Zr-4合金沖制過程中變形機制的開啟情況。從圖6中選取3個典型位置(凹模圓角、斜壁和凸模圓角),每個位置選取3種典型取向,共9個晶粒分別標記為G1~G9(紅色-G1/G4/G7;綠色-G2/G5/G8;藍色-G3/G6/G9),然后對其進行IGMA分布特征的分析,如圖10所示。其中,凹模圓角中紅色晶粒G1取向為近基極取向,IGMA分布的旋轉軸主要集中在<0001>軸,說明其以柱面滑移為主;隨著c軸向TD方向偏轉,以綠色(G2)和藍色(G3)為代表的非基極取向晶粒的IGMA強度極點出現在了<138?5?3>軸和<61?5?3>軸附近,說明此時在單向拉伸的應變路徑條件下,Zr-4合金變形以柱面滑移系為主,錐面滑移系為輔,同時也發現存在極點集中在<1?21?0>,表明少量基面滑移會開啟,并結合前面少量的孿晶生成,可知協調厚度方向變形的變形機制主要是錐面滑移,基面滑移和孿生次之。與凹模圓角類似,當斜壁位置處晶粒的c軸與法線方向平行時(G4),其IGMA分布的旋轉軸主要集中在<0001>軸,而對于c軸近似垂直于ND的TD取向晶粒(G5和G6),晶粒的IGMA分布特征落在內扇形上,說明仍是以柱面滑移主導,錐面滑移協調變形的機制。凸模圓角處的紅色取向晶粒(G7)的IGMA強度極點分布出現了發散的跡象,不只在<0001>軸集中,同時向扇形邊緣處發生擴散,G8和G9晶粒的IGMA的強度極點也出現發散的跡象,并且主要彌散分布于扇形邊緣處,沿著的分布強度逐漸升高,說明基面滑移開啟被促進,柱面滑移的開啟受到了抑制,而此位置主要開啟基面滑移以協調厚度方向上的變形,與凹模圓角和斜壁不同。平面應變路徑促進了基面滑移系的開啟,而基面滑移的開啟使得c軸從TD方向偏轉到ND方向,逐漸從基面的雙峰織構向基面發生織構集中,進而導致凸模圓角位置最終發生沖制開裂。

3.2基于VPSC預測沖制過程中變形機制
利用VPSC模型預測了沖制過程中織構的演變和滑移系開啟的變化規律,選取圖1所示的織構作為變形前的初始織構,采用有限元中提取的隨時間變化的正應變結果作為變形邊界條件。實驗與VPSC預測的(0001)織構及Kearns系數結果對比如圖11所示。VPSC模擬結果很好地捕獲了實驗結果中的織構特征,驗證了模型的準確性。如圖11a和b所示,當位于凹模圓角時,織構發生了輕微的變化。其中,實驗的孿晶產生量為1.896%,VPSC預測的孿晶激活分數為1.66%。無論是實驗結果還是預測結果,織構的變化趨勢相似,均是近基極取向的母晶產生孿晶,使Fr略微增大,產生了新的織構類型。斜壁位置預測的織構和實驗織構均由于應變太小,沒有發生明顯的變化,變形后的織構保持了典型的軋制雙峰織構(圖11c和d)。與初始織構相比,凸模圓角位置Fn的實驗值和VPSC預測值均增大,Ft降低,Fr略微增大。表明晶粒取向從TD向ND偏轉,使得變形后織構發生了集中,進而造成了織構強度的增大。
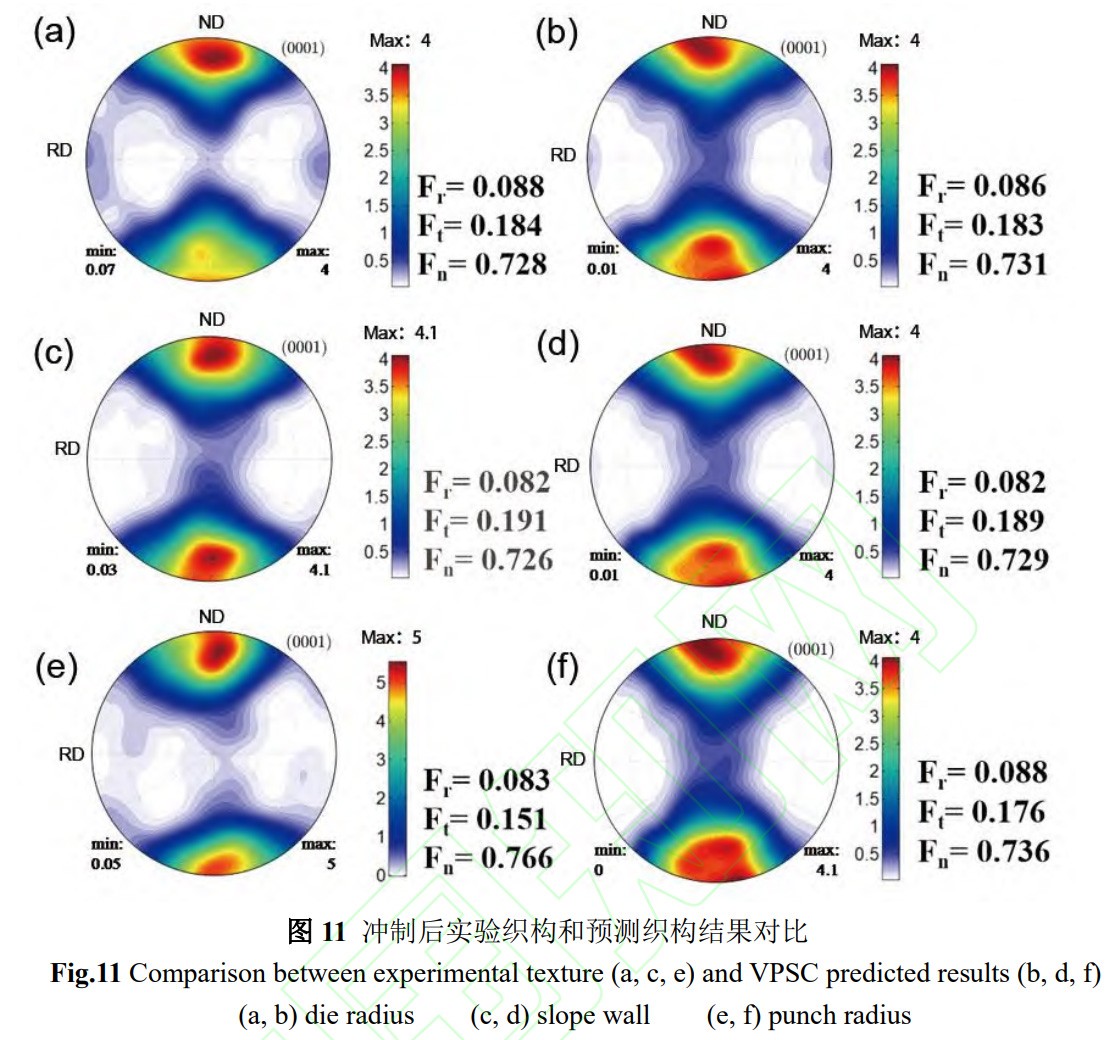
圖12所示為沖制過程VPSC預測的變形機制開啟情況。如圖12a所示,凹模圓角位置的柱面滑移最容易開啟,錐面滑移作為協調厚度方向上變形的主要輔助滑移系,這一結果與IGMA分析結果相同。隨著應變的增大,柱面滑移和錐面滑移開啟降低,基面滑移開啟增大,但開啟量不會超過錐面滑移。此外,預測的ETW開啟量為1.66%,這與實驗中統計的孿晶生成量吻合得很好。
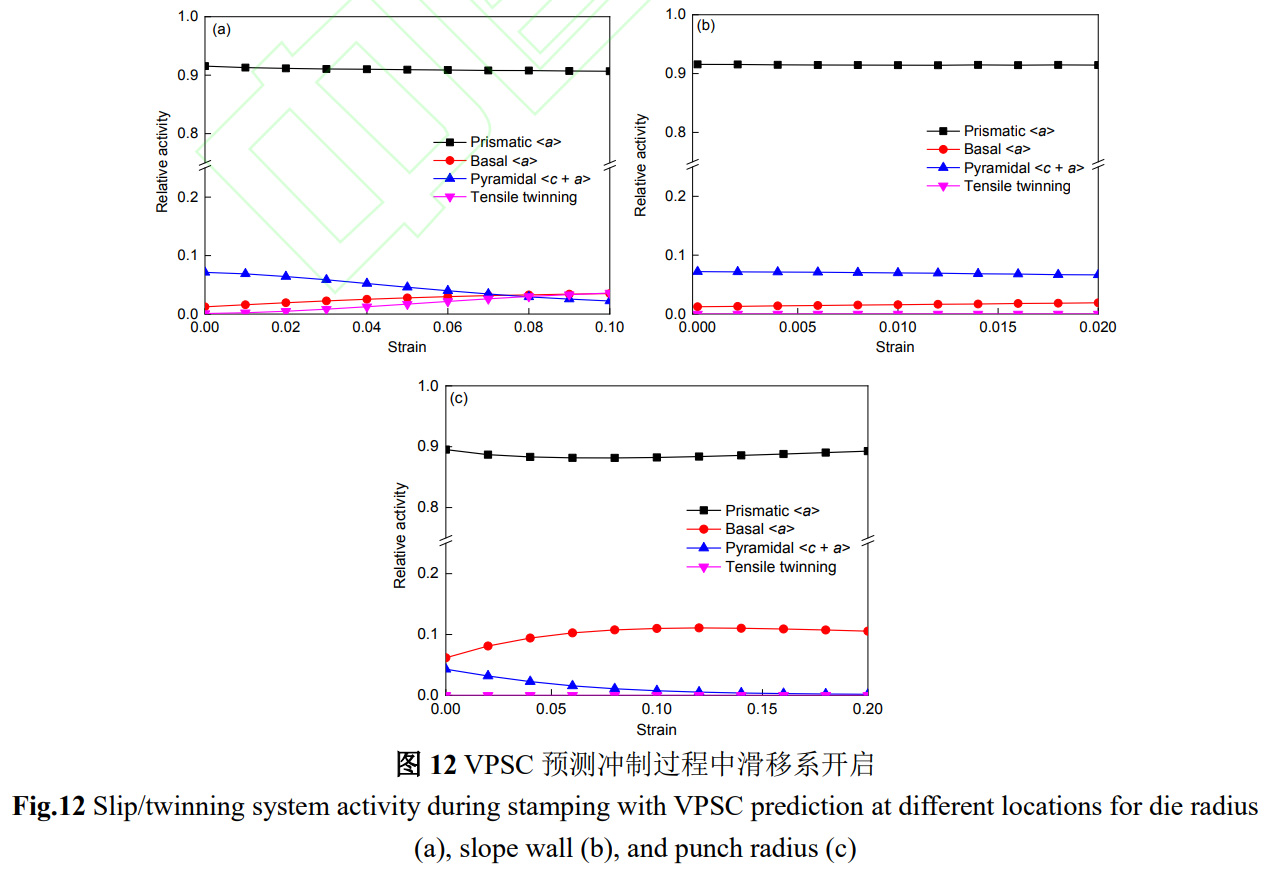
斜壁段的變形機制以柱面滑移為主,錐面滑移為輔(圖12b)。通過對比可知,柱面滑移的相對開啟量最高,由于錐面滑移在此變形條件下激活量更高,所以基面滑移幾乎不開啟,孿生也不開啟。與單向拉伸變形的織構演變類似,在柱面滑移與錐面滑移配合開啟的條件下,變形織構與初始織構相似,不會產生明顯的織構變化。凸模圓角位置的Kearns系數Fr幾乎沒有變化,Ft減小,Fn增大,說明c軸從TD方向繼續向ND方向偏轉。通過VPSC對變形機制激活量的預測可知,受到平面應變路徑的影響,柱面滑移受到抑制,低于凹模圓角和斜壁,基面滑移的開啟量高于錐面滑移,成為了該路徑下協調厚度變形的滑移系。隨著沖制過程的進行,應變的增大,基面滑移系開啟不斷增加,錐面滑移系不斷降低,只產生了微量的孿晶。說明基面滑移隨著變形程度的增加成為了唯一協調厚度方向變形的滑移,其開啟量的增大使得初始的雙峰織構轉為近基面織構,織構強度不斷升高,當基面滑移的開啟量達到臨界值時,厚度方向協調變形困難,進而發生破裂,也就是說,凸模圓角處發生破裂是由于基面滑移系大量開啟導致。
4、結論
(1)針對Zr-4合金帶材(0.457mm)進行沖制實驗,當凸模圓角R=0.15mm,Zr-4合金帶材沖制變形深度為1.16mm時,帶材發生破裂,破裂位置位于凸模圓角處。
(2)沖制后沿縱截面3個位置的織構實驗結果表明,相較于初始織構,凹模圓角位置由于ETW產生了沿RD方向的新織構,使得Fr增大,Ft降低;斜壁位置的變形織構與初始織構相似;凸模圓角位置從雙峰織構轉為近基面織構,Fn增大,Fr增大,而Ft降低。
(3)采用FEM預測沖制變形時,斜壁和凹模圓角位置的應變路徑為單向拉伸,凸模圓角位置為平面應變路徑。
(4)在斜壁位置的單向拉伸應變路徑,變形機制以柱面滑移開啟為主,錐面滑移為輔,由于變形較小,織構沒有發生明顯的變化;凹模圓角位置處,變形機制仍然以柱面滑移主導,錐面滑移和ETW共同協調變形,使得織構產生了從ND向RD方向偏轉的新織構類型。
(5)平面應變路徑抑制了柱面滑移和錐面滑移的開啟,促進了基面滑移協調變形,基面滑移的開啟使織構從雙峰織構轉變為近基面織構。隨著應變的增大,基面滑移成為了唯一協調厚度變形的滑移系,當其開啟量達到臨界時,厚度方向難以協調變形,沖制發生開裂。可見,基面滑移是影響沖制開裂的關鍵變形機制。
參考文獻
[1] Han E H. Research trends on micro and nano-scale materials degradation in nuclear power plant [J]. Acta Metall. Sin., 2011, 47: 769
(韓恩厚. 核電站關鍵材料在微納米尺度上的環境損傷行為研究——進展與趨勢 [J]. 金屬學報, 2011, 47: 769)
[2] Murty K L, Charit I. Texture development and anisotropic deformation of zircaloys [J]. Prog. Nucl. Energy, 2006, 48: 325
[3] Ren Q Y, Chen J, Zhao R R, et al. Mechanical performance of newly developed supporting structure of spacer grid [J]. At. Energy Sci. Technol., 2020, 54: 2411
(任全耀, 陳 杰, 趙瑞瑞等. 新型定位格架夾持結構的力學特性研究 [J]. 原子能科學技術, 2020, 54: 2411)
[4] Akhtar A, Teghtsoonian A. Plastic deformation of zirconium single crystals [J]. Acta Metall., 1971, 19: 655
[5] McCabe R J, Cerreta E K, Misra A, et al. Effects of texture, temperature and strain on the deformation modes of zirconium [J]. Philos. Mag., 2006, 86A: 3595
[6] Akhtar A. Prismatic slip in zirconium single crystals at elevated temperatures [J]. Metall. Trans., 1975, 6A: 1217
[7] Li Y, Po G, Cui Y N, et al. Prismatic-to-basal plastic slip transition in zirconium [J]. Acta Mater., 2023, 242: 118451
[8] Knezevic M, Zecevic M, Beyerlein I J, et al. Strain rate and temperature effects on the selection of primary and secondary slip and twinning systems in HCP Zr [J]. Acta Mater., 2015, 88: 55
[9] McCabe R J, Proust G, Cerreta E K, et al. Quantitative analysis of deformation twinning in zirconium [J]. Int. J. Plast., 2009, 25: 454
[10] Lei C Y, Mao J Z, Zhou D W, et al. Effects of annealing treatments on forming performance of zirconium alloys [J]. Trans. Nonferrous Met. Soc. China, 2022, 32: 2908
[11] Deng Z P, Zhou D W, Jiang P S, et al. Optimization on stamping process parameters for zirconium alloy sheet strip based on orthogonal experiment [J]. Forg. Stamping Technol., 2019, 44(9): 12
(鄧振鵬, 周惦武, 蔣朋松等. 基于正交試驗的鋯合金薄板帶材沖壓工藝參數優化 [J]. 鍛壓技術, 2019, 44(9): 12)
[12] Lei C Y, Mao J Z, Zhang X M, et al. A comparison study of the yield surface exponent of the Barlat yield function on the forming limit curve prediction of zirconium alloys with M-K method [J]. Int. J. Mater. Form., 2021, 14: 467
[13] Kim M, Bang S, Lee H, et al. Enhancement of dimple formability in sheet metals by 2-step forming [J]. Mater. Des. (1980-2015), 2014, 54: 121
[14] Marimuthu K P, Choi W, Kim N, et al. Numerical investigations on the effect of pit on two-step dimple forming of atomic fuel spacer grid [J]. Int. J. Adv. Manuf. Technol., 2018, 94: 293
[15] Deng S Y, Song H W, Liu H, et al. Effect of uniaxial loading direction on mechanical responses and texture evolution in cold pilgered Zircaloy-4 tube: experiments and modeling [J]. Int. J. Solids Struct., 2021, 213: 63
[16] Liu H, Deng S Y, Chen S F, et al. Correlation of the anisotropic hardening behavior and texture features of cold rolled Zr-4 sheet under uniaxial tension [J]. J. Mater. Sci. Technol., 2022, 119: 111
[17] Luan B F, Gao S S, Chai L J, et al. Compression deformation behavior of Zr–1Sn–0.3Nb alloy with different initial orientations at 650 °C [J]. Mater. Des. (1980-2015), 2013, 52: 1065
[18] Chen J W, Luan B F, Chai L J, et al. Heterogeneous microstructure and texture evolution during fabrication of Zr-Sn-Nb zirconium alloy sheets [J]. Acta Metall. Sin., 2012, 48: 393
(陳建偉, 欒佰峰, 柴林江等. Zr-Sn-Nb 新型鋯合金板材加工過程中不均勻組織與織構演變 [J]. 金屬學報, 2012, 48: 393)
[19] Knezevic M, Beyerlein I J, Nizolek T, et al. Anomalous basal slip activity in zirconium under high-strain deformation [J]. Mater. Res. Lett., 2013, 1: 133
[20] Cao Y C, Chen D, Xia L, et al. Effects of primary α grains on rolling reductions and deformation modes in Zr alloys: Experiments and modeling [J]. Mech. Mater., 2024, 19: 104957
[21] Kearns J J. On the relationship among ‘f’ texture factors for the principal planes of zirconium, hafnium and titanium alloys [J]. J. Nucl. Mater., 2001, 299: 171
[22] Su R, Liu J Y, Qiao X Y, et al. Advances in scanning white light interferometry for surface topography measurement [J]. Laser Optoelectron. Prog., 2023, 60: 0312005
(蘇 榕, 劉嘉宇, 喬瀟悅等. 用于表面形貌測量的掃描白光干涉技術進展 [J]. 激光與光電子學進展, 2023, 60: 0312005)
[23] Akhtar A. Compression of zirconium single crystals parallel to the c- axis [J]. J. Nucl. Mater., 1973, 47: 79
[24] Akhtar A. Basal slip in zirconium [J]. Acta Metall., 1973, 21: 1
[25] Chun Y B, Battaini M, Davies C H J, et al. Distribution characteristics of in-grain misorientation axes in cold-rolled commercially pure titanium and their correlation with active slip modes [J]. Metall. Mater. Trans., 2010, 41A: 3473
相關鏈接






















